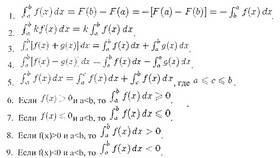В математическом анализе сумма интегралов подчиняется определенным правилам и обладает важными свойствами, которые широко используются при решении задач. Рассмотрим эти закономерности подробно.
Содержание
В математическом анализе сумма интегралов подчиняется определенным правилам и обладает важными свойствами, которые широко используются при решении задач. Рассмотрим эти закономерности подробно.
Основное свойство аддитивности интегралов
Для любых интегрируемых функций f(x) и g(x) на отрезке [a, b] выполняется:
∫[a,b] (f(x) + g(x)) dx = ∫[a,b] f(x) dx + ∫[a,b] g(x) dx
Свойства суммы интегралов
| Свойство | Формулировка |
| Линейность | ∫(αf(x) + βg(x))dx = α∫f(x)dx + β∫g(x)dx |
| Аддитивность по промежутку | ∫[a,c] f(x)dx = ∫[a,b] f(x)dx + ∫[b,c] f(x)dx |
| Сумма определенных интегралов | ∫f(x)dx + ∫g(x)dx = ∫(f(x)+g(x))dx + C |
Примеры вычисления суммы интегралов
Пример 1: Простая сумма
Вычислим ∫(2x + 3)dx:
- ∫2x dx = x² + C₁
- ∫3 dx = 3x + C₂
- Сумма: x² + 3x + C (где C = C₁ + C₂)
Пример 2: Определенные интегралы
Вычислим ∫[0,1] (x² + x) dx:
- ∫[0,1] x² dx = 1/3
- ∫[0,1] x dx = 1/2
- Сумма: 1/3 + 1/2 = 5/6
Применение в физике
Сумма интегралов часто встречается при расчете:
- Работы силы (сумма элементарных работ)
- Центра масс системы тел
- Электрического потенциала от нескольких зарядов
Важное замечание
При сложении неопределенных интегралов константы интегрирования можно объединять, так как сумма двух произвольных констант дает новую произвольную константу.
Вывод
Свойство аддитивности интегралов значительно упрощает вычисления и позволяет разбивать сложные задачи на более простые. Понимание этого принципа необходимо для решения широкого круга математических и физических задач.
